Question

HELP ASAP
photo attached

Answer 1

D. undefined

General Formulas and Concepts:

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Trig Derivative:
`\displaystyle (d)/(dx)[sinu] = u'cosu`

Derivatives of Parametrics:
`\displaystyle (dy)/(dx) = ((dy)/(dt))/((dx)/(dt))`

Explanation:

Step 1: Define

`\displaystyle (dx)/(dt) = 5`

`\displaystyle (dy)/(dt) = sin(t^2)`

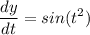
Step 2: Differentiate

1. [x Derivative] Basic Power Rule:
   `\displaystyle (d^2x)/(dt^2) = 0`
2. [y Derivative] Trig Derivative [Chain Rule]:
   `\displaystyle (d^2y)/(dt^2) = cos(t^2) \cdot (d)/(dt)[t^2]`
3. [y Derivative] Basic Power Rule:
   `\displaystyle (d^2y)/(dt^2) = cos(t^2) \cdot 2t^(2 - 1)`
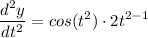
4. [y Derivative] Simplify:
   `\displaystyle (d^2y)/(dt^2) = 2tcos(t^2)`
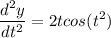
5. [Derivative] Rewrite:
   `\displaystyle (d^2y)/(dx^2) = (2tcos(t^2))/(0)`

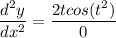
Anything divided by 0 is undefined.

Topic: AP Calculus BC (Calculus I/II)

Unit: Differentiation with Parametrics

Book: College Calculus 10e