Question

find the equation of the straight line passing through P -2,1and parallel to the line with equation 2x - 3y=1​

Answer 1

`y=(2)/(3) x+(7)/(3)`

Explanation:

Parallel lines have the same slope. Therefore, the line we're trying to find the equation for and the given line 2x-3y=1​ must have the same slope.

1) Find the slope of 2x-3y=1​

To do this, rewrite this equation in slope-intercept form:
`y=mx+b` where
`m` is the slope and
`b` is the y-intercept (the value of y when the line crosses the y-axis)

`2x-3y=1`

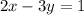
Subtract 2x from both sides

`2x-3y-2x=1-2x\\-3y=-2x+1`

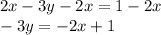
Divide both sides by -3 to isolate y

`(-3y)/(-3)=(-2)/(-3)x+((1)/(-3) )\\y=(2)/(3)x-(1)/(3)`

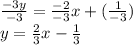
Now, we can easily identify that
`(2)/(3)` is in the position of m, the slope. Plug this into
`y=mx+b`:

`y=(2)/(3) x+b`

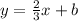
2) Find the y-intercept

`y=(2)/(3) x+b`

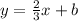
To find the y-intercept, plug the given point P(-2,1) into the equation and solve for b

`1=(2)/(3) (-2)+b\\1=(-4)/(3)+b`

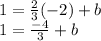
Add
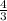`(4)/(3)` to both sides of the equation

`1+(4)/(3)= (-4)/(3) +b+(4)/(3) \\(3)/(3) +(4)/(3)= b\\(7)/(3)`

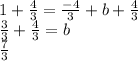
Therefore, the y-intercept of the line is
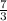`(7)/(3)`. Plug this into our original equation:

`y=(2)/(3) x+b\\y=(2)/(3) x+(7)/(3)`

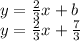
I hope this helps!