Question

11. Albert has 12 more 10 cent coins than 20-cent

coins. The total value of all his coins is $5.40. Find
the total number of coins he has.

Answer 1

in total he has 62 cents

Explanation:

I hope it's the correct answer if I'm wrong tell me right away.

Answer 2

Explanation:

Let x be the number of 10 cent coins

Let y be the number of 20 cent coins

given

`x = y + 12 \\ x - y = 12`

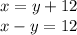
as equation 1

and

`0.1x + 0.2y = 5.4`

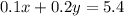
as equation 2.

Now we will use elimination method to solve simultaneous equations.

Now we multiply equation 1 by 0.2 to eliminate y and solve for x first.

`0.2 * x - 0.2 * y = 12 * 0.2 \\ 0.2x - 0.2y = 2.4`

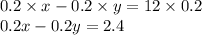
Let this new equation be equation 3.

Now use equation 2 + equation 3.

`0.1x + 0.2x + (0.2y + ( - 0.2y)) = 5.4 + 2.4 \\ 0.3x = 7.8 \\ x = 7.8 / 0.3 \\ = 26`

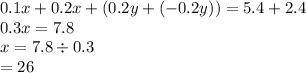
Substitute x into equation 1,

`x = y + 12 \\ y + 12 = x \\ y = x - 12 \\ = 26 - 12 \\ = 14`

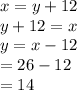
Therefore total number of coins = x + y = 26 + 14 = 40