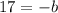Answer:
Other root of equation,
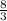
Value of (
 ),
),
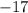
Explanation:
The given quadratic equation is in standard form. Standard form is the basic format of representing a quadratic equation, a quadratic equation in standard form would use the following format,
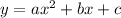
To solve this problem, one could use Vieta's theorems. Vieta's theorems state the following, let (
 ) and (
) and (
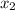 ) represent the roots of the equation,
) represent the roots of the equation,
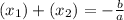
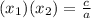
Substitute the given values into the equation,
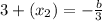
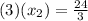
Simplify,
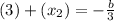
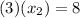
Inverse operations,
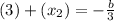
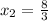
Substitute in the value of (
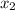 ),
),
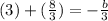
Simplify, convert to improper fractions and combine like terms,
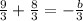
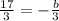
Multiply both sides of the equation by (
 ) to remove the denominator,
) to remove the denominator,