Question

A day on a distant planet observed orbiting a nearby star is 21.5 hr. Also, a year on the planet lasts 69.3 Earth days. In other words, for the purposes of unit conversion, there are 24 hr in a day, 60 min in an hour, and 60 s in a minute, as it would for astronomers on Earth observing the planet. Calculate the average angular speed of the planet about its own axis of rotation in radians per second, with the second as measured on Earth. what is the speed of rotation? Calculate the average angular speed of the planet as it travels around its neighboring star, with the second as measured on Earth. what is the speed of orbit?

Answer 1

Part A

The angular speed of rotation of the plane is 8.11781 × 10⁻⁵ rad/s

Part B

The angular speed of orbit of the planet is 1.04938 × 10⁻⁶ rad/s

Step-by-step explanation:

The parameters of the planet are;

The duration of a day on the distant planet = 21.5 hr.

The duration of a year on the distant planet = 69.3 Earth days

Part A

The duration of a day = The time to make one complete revolution of 2·π radians

∴ The average angular speed about its axis,
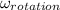`\omega_(rotation)` = Angle turned/Time

∴
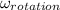`\omega_(rotation)` = 2·π/(21.5 × 60 × 60) s ≈ 8.11781 × 10⁻⁵ rad/s

The average angular speed of the planet about its own axis,
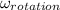`\omega_(rotation)` = 8.11781 × 10⁻⁵ rad/s

The angular speed of rotation of the plane
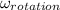`\omega_(rotation)` = 8.11781 × 10⁻⁵ rad/s

Part B

The time it takes the planet to revolve round the neighboring star once = 69.3 Earth days

Therefore, the average angular speed of the planet around its neighboring star,
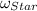`\omega _(Star)`, is given as follows;

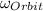`\omega _(Orbit)` = 2·π/((69.3 × 24 × 60 × 60) s) = 1.04938 × 10⁻⁶ rad/s

The average angular speed of orbit,
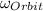`\omega _(Orbit)` = 1.04938 × 10⁻⁶ rad/s

The angular speed of orbit of the planet,
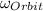`\omega _(Orbit)` = 1.04938 × 10⁻⁶ rad/s.