Answer:
B.
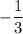
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Algebra I
- Terms/Coefficients
- Exponential Rule [Rewrite]:
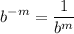
- Exponential Rule [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/2022/formulas/mathematics/college/yqpyvbuov0tgbjo8vla0qsqp67pafn2fr7.png)
Calculus
Derivatives
Derivative Notation
Derivative of a constant is 0
The definition of a derivative is the slope of the tangent line
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Implicit Differentiation
Explanation:
Step 1: Define
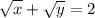
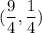
Step 2: Differentiate
Implicit Differentiation
- [Function] Rewrite [Exponential Rule - Root Rewrite]:
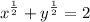
- [Function] Basic Power Rule:
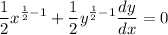
- [Derivative] Simplify:
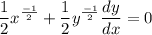
- [Derivative] Rewrite [Exponential Rule - Rewrite]:
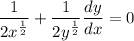
- [Derivative] Isolate
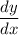 term [Subtraction Property of Equality]:
term [Subtraction Property of Equality]:
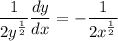
- [Derivative] Isolate
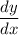 [Multiplication Property of Equality]:
[Multiplication Property of Equality]:
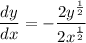
- [Derivative] Simplify:
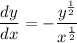
Step 3: Evaluate
Find slope of tangent line
- Substitute in point [Derivative]:
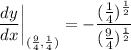
- [Slope] Exponents:
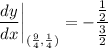
- [Slope] Simplify:
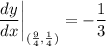
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Differentiation - Implicit Differentiation
Book: College Calculus 10e