Answer:
a. Above 337.8 grams.
b. Between 318.25 grams and 331.75 grams.
c. Above 316.59 grams.
d. Below 312.2 grams
Explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of 325 grams and a standard deviation of 10 grams.
This means that
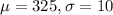
a. Highest 10 percent
This is X when Z has a pvalue of 1 - 0.1 = 0.9, so X when Z = 1.28.

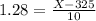
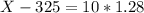
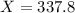
So 337.8 grams.
b. Middle 50 percent
Between the 50 - (50/2) = 25th percentile and the 50 + (50/2) = 75th percentile.
25th percentile:
X when Z has a pvalue of 0.25, so X when Z = -0.675.

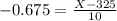
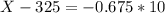
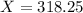
75th percentile:
X when Z has a pvalue of 0.75, so X when Z = 0.675.

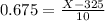
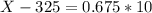
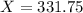
Between 318.25 grams and 331.75 grams.
c. Highest 80 percent
Above the 100 - 80 = 20th percentile, which is X when Z has a pvalue of 0.2. So X when Z = -0.841.

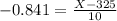
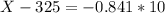
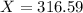
Above 316.59 grams.
d. Lowest 10 percent
Below the 10th percentile, which is X when Z has a pvalue of 0.1, so X when Z = -1.28.

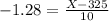
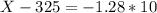
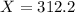
Below 312.2 grams