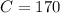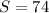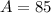Answer:
170 children
74 students
85 adults
Explanation:
Given
Let:
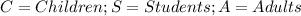
For the capacity, we have:

For the tickets sold, we have:
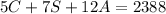
Half as many as adults are children implies that:

Required
Solve for A, C and S
The equations to solve are:
 -- (1)
-- (1)
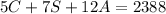 -- (2)
-- (2)
 -- (3)
-- (3)
Make C the subject in (3)
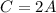
Substitute
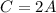 in (1) and (2)
in (1) and (2)
 -- (1)
-- (1)
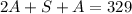
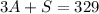
Make S the subject
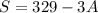
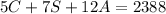 -- (2)
-- (2)
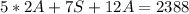
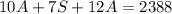
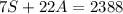
Substitute
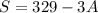
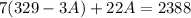
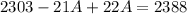
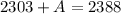
Solve for A
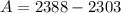
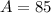
Recall that:
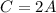
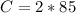
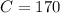
Recall that:
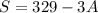
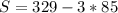

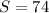
Hence, the result is: