Question

The figure shows a person estimating the height of a tree by looking at the

top of the tree with a mirror. Assuming that both the person and the tree form
right angles with the ground, which of the following proportions can be used
to estimate the height of the tree?

Answer 1

The proportion that can be used to estimate the height of the tree is option;

A.
`(h)/(12) = (6)/(5)`

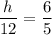
Explanation:

The given parameters in the question are;

The medium through which the person looks at the top of the tree = A mirror

The angle formed by the person and the tree with the ground = Right angles = 90°

The distance of the person from the mirror, d₁ = 5 ft.

The height of the person, h₁ = 6 ft.

The distance of the tree from the mirror, d₂ = 12 ft.

The angle formed by the incident light from the tree on the mirror, θ₁ = The angle of the reflected light from the mirror to the person, θ₂

Let 'A', 'B', 'M', 'T', and 'R' represent the location of the point at the top of the person's head, the location of the point at the person's feet, the location of the mirror, the location of the top of the tree and the location of the root collar of the tree, we have;

TR in ΔMRT = The height of the tree = h, and right triangles ΔABM and ΔMRT are similar

The corresponding legs are;

The height of the person and the height of the tree, which are AB = 6 ft. and TR = h, respectively

The distances of the person and the tree from the mirror, which are BM = 5 ft. and MR = 12 ft. respectively

∴ The angle formed by the incident light from the tree on the mirror, θ₁ = ∠TMR

The angle of the reflected light from the mirror to the person, θ₂ = ∠AMB

Given that θ₁ = θ₂, we have;

tan(θ₁) = tan(θ₂)

∴ tan(∠TMR) = tan(∠AMB)

`tan\angle X = (Opposite \ leg \ length \ to \ reference \ angle)/(Adjacent \ leg \ length \ to \ reference \ angle)`

`tan(\angle TMR) = (TR)/(MR) = (h)/(12)`

`tan(\angle AMB) = (AB)/(BM) = (6)/(5)`

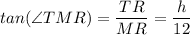
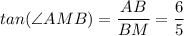
From tan(∠TMR) = tan(∠AMB), we have;

`(h)/(12) = (6)/(5)`

`\therefore h = (6 \, ft.)/(5 \, ft.) * 12 \, ft. = 14.4 \, ft.`

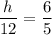
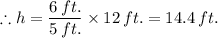
The height of the tree, h = 14.4 ft.

Therefore, from the proportion
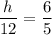`(h)/(12) = (6)/(5)` the height of the tree can be estimated.