Question

Helppp law of sines and law of cosines

Answer 1

Explanation:

In this case, you would use law of sines due due you being given two angles and one side.

LAW OF ANGLES IN TRIANGLES: 180 - a - b = c

So in this case: 180 - 31 - 58 = m<S = 91

LAW OF SINE: sin A / a = sin B / b = sin C / c

So in this case: sin 31 / ST = sin 58 / 28

28 sin 31 / sin 58 = ST = 17.0

sin 58 / 28 = sin 91 / x

28 sin 91 / sin 58 = RT = 33.0

Answer 2

`\displaystyle ST ≈ 15,9\\ RT ≈ 30,8 \\ m∠S = 111°`

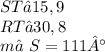
Explanation:

First off, find
`\displaystyle m∠S:`

`\displaystyle 180° = 58° + 31° + m∠S → 180° = 89° + m∠S \\ 111° = m∠S`

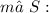
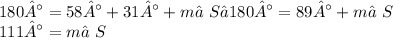
Now that the third angle has been defined, we can move move forward with solving for a second edge, using the Law of Sines, but before proceeding, here are some things you should know about this triangle:

• Edge s [RT] →
  `\displaystyle m∠S`
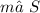
• Edge t [RS] →
  `\displaystyle m∠T`
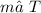
• Edge r [ST] →
  `\displaystyle m∠R`

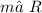
Now that we have the information, we can proceed with the process:

`\displaystyle (t)/(sin∠T) = (s)/(sin∠S) = (r)/(sin∠R) \\ \\ (28)/(sin\:58°) = (s)/(sin\:111°) → (28sin\:111°)/(sin\:58°) → 30,82402055... = s \\ 30,8 ≈ s`

_______________________________________________

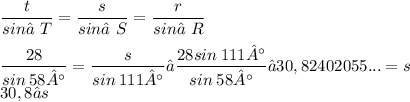
Now that RT has been defined, we can now proceed to solving the third edge, using the Law of Cosines:

`\displaystyle s^2 + r^2 - 2sr\: cos∠T = t^2 \\ t^2 + r^2 - 2tr\: cos∠S = s^2 \\ t^2 + s^2 - 2ts\: cos∠R = r^2 \\ \\ 28^2 + 30,8^2 - 2[28][30]\: cos\:31° = r^2 → 784 + 948,64 - 1680\: cos\:31° = r^2 → √(254,1978397...) = √(r^2) → 15,94358303... = r \\ 15,9 ≈ r`

Your triangle is now complete!

I am joyous to assist you at any time.