Question

How many atoms are in 25.00 g of B?

A. 1.393 x 10^24 atoms of B
B. 1.333 x 10^23 atoms of B
C. 2.16 x 10^26 atoms of B
D.217 x 10^24 atoms of B
Thanks for all the efforts :)

Answer 1

There are 1.393 x 10²⁴ atoms in 25.00 g of B.

Step-by-step explanation:

Hey there!

We are given a value, in grams, that we need to convert to a number of atoms.

We can convert grams to atoms by using Avogadro's Number (
`N_A`). This number is equivalent to
`6.022 * 10^(23)`.

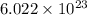This number can be used to convert any values to:

• atoms
• molecules
• formula units
• moles

In order to do this problem, we will need to use dimensional analysis (DA). This process allows us to convert from grams to atoms.

We need to set up our ratios in order to work this out. We can use a periodic table to help us through this next part of the problem.

1. Locating the number of moles of B in the sample

We first need to find the amount of moles of boron (B) there are in the sample.

Checking a periodic table, the atomic mass in atomic mass units (amu) is 10.81 amu.

• Atomic mass units can easily be converted to grams and these units can be used interchangeably.

Therefore, for each atom of boron, it weighs 10.81 grams to us. This is equivalent to the mass of one mole of boron.

To find the number of moles, we have two possible ratios we can use:

• 
  `\displaystyle (1 \ mole \ B)/(10.81 \ grams \ B)`

• 
  `\displaystyle (10.81 \ grams \ B)/(1 \ mole \ B)`

These ratios mean the same thing, but we need to convert our final unit to moles.

We are given a sample in grams, and when dividing our units, we need to keep moles.

Since the first portion of our expression is in grams, we need to have grams in the bottom of our expression.

• 
  `\displaystyle 25.00 \ \text{grams B} \ * \frac{1 \text{mole B}}{10.81 \ \text{grams B}}`

We can now simplify the expression. Our grams B unit will cancel out, so we are therefore left with moles B remaining.

2. Locating the number of atoms in the sample

Now with our equation, we can convert our number of moles that would be solved if we stopped with the above. However, we need to convert to atoms.

We use Avogadro's number and create a ratio with that of moles.

• 
  `\displaystyle \frac{6.022 * 10^(23)\text{atoms}}{1 \text{mole B}}`

• 
  `\displaystyle \frac{1 \text{mole B}}{6.022 * 10^(23) \text{atoms}}`

We need to cancel out our moles and end with atoms, so we must have moles in the denominator. Therefore, we use the first ratio.

Using our previous expression, we multiply by this new ratio and solve the expression.

• 
  `\displaystyle 25.00 \ \text{grams B} \ * \frac{1 \text{mole B}}{10.81 \ \text{grams B}} \ * \frac{6.022 * 10^(23)\text{atoms}}{1 \text{mole B}}`

This expression can now be operated. You will need a calculator to perform this calculation.

Our numerator is:

• 
  `[(25.00 * 1 * (6.022 * 10^(23))]`

Plugging this into a calculator, we get:

• 
  `1.5055 * 10^(25)`

Our denominator is:

• 
  `(1 * 10.81 * 1)`

This simplifies to:

• 
  `10.81`

Dividing our numerator and denominator:

• 
  `\displaystyle (1.5055 * 10^(25))/(10.81)`

Plugging this into a calculator, we get:

• 
  `1.392691952 * 10^(24)`

3. Simplifying with significant figures

Now, we need to take into account that we have significant figures. We are given this original value:

• 
  `25.00`

This value has four significant figures, which means we need to round our value we received above to four significant figures.

• 
  `\approx 1.393`

Our units are added as well as our scientific notation:

• 
  `1.393 * 10^(24) \ \text{atoms of B}`

Therefore, our final answer is choice A.