Given:
Entrance fee = $5.50
Additional fee = $1.25 for each activity.
Total amount spend at fair = $30
To find:
The equation that represents the problem.
Solution:
Let the number of activities be
 .
.
Additional fee for 1 activity =
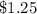
Additional fee for x activity =
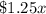
Total fee = Entrance fee + Additional fee for x activity
=
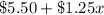
It is given that Kevin has at most $30 to spend at the fair. So, total fee must be equal to $30.
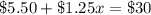

Therefore, the require equation is
 .
.
Note: The inequality for the given problem is
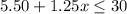 .
.