Question

i have been trying to solve this compound and double angle question please help me find the answer to these question guys​

Answer 1

These type of questions are super tricky b/c you have to remember all the different versions of the identities, and then they put the question in some odd form, I feel like this should land math professors in jail , for dishonesty , b/c it's really a form of "how tricky can I make a question and still have a way to solve it" anyway,

Explanation:

a)

next the question asks 1-cos 2A and this is total abuse of notation. the way this should be written is 1- cos( 2A) so we know that the A is part of the cosine functions input... btw.. in any computer program, it would never ever let you get away with that top form of the expression. :/ anyway... I keep ranting.. huh... sorry :P

1-cos(2A) is an odd form of the identity 1/2(1-cos(2A) =
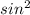`sin^(2)`(A) the 1/2 is missing but we can add that pretty easy, we just have to remember to take it out too. I usually forget to do that. and my professor marks me off completely, totally wrong, but I just miss one small thing :/ anyway....

our 1-cos(2A) needs the 1/2 added to it. or if we move that 1/2 to the other side it looks like 2*
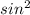`sin^(2)`(A) = 1-cos(2A) and this is that "odd" from of the identity that I was talking about.

next let's deal with sin(2A) it has an identity of 2 sin(A)cos(A) which is really nice for us b/c it will cancel out the 2 in then numerator for us, nice !

now our fraction looks like [2*
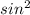`sin^(2)`(A)] / 2 sin(A)cos(A)

so cancel out one of the sines

2*sin(A) / 2 cos(A)

cancel the 2s

Sin(A) / Cos(A) = Tan(A)

nice it worked out :P

b)

by the above that we just worked out, then

Tan(15) = Sin(15) / Cos(15)

I had to look up what sin of 15 is b/c it's not one of those special angles but it does have an exact form of

Sin(15) = (√3 - 1) / 2√2

Cos(A) = (√3 + 1) / 2√2

you can use rule of Cos(A-B) = Cos(A)Cos(B)+Sin(A)Sin(B) to get the above and a similar rule for Sin(A-B)

back to our problem, the 2√2 will cancel out

then we have

Tan(15) = (√3 - 1) /(√3 + 1)

in the form that is above that's exact, the roots could be approximated but i'll just leave that in the form that is exact. Most math professors like that form.