James is solving a number puzzle that involves three integers, a, b, and c, where c is a positive integer. The product of a and b is 6. The product of a and c is -4. The product…

Question

asked Jun 5, 2022 196k views

1 Answer

TorukMakto · Answer 1 · 2022-06-09T23:48:23+0000

Given:

Three integers, a, b, and c, where c is a positive integer.

The product of a and b is 6.

The product of a and c is -4.

The product of b and c is -6.

To find:

The values of a,b and c.

Solution:

According to the given information:

ab=6 ...(i)

ac=-4 ...(ii)

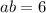bc=-6 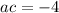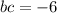...(iii)

From (ii), we get

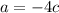$a=-\dfrsc{4}{c}$ ...(iv)

From (iii), we get

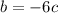$b=-\dfrsc{6}{c}$ ...(v)

Putting
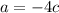$a=-\dfrsc{4}{c}$ and
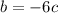$b=-\dfrsc{6}{c}$ in (i), we get

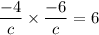
(-4)/(c)* (-6)/(c)=6

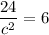
(24)/(c^2)=6

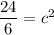
(24)/(6)=c^2

4=c^2

Taking square root on both sides, we get

$\pm √(4)=c$

$\pm 2=c$

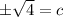
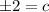
It is given that c is a positive integer. So, it cannot be negative and the only value of c is
c=2 .

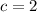Putting
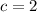c=2 in (iv), we get

$a=-\dfrsc{4}{2}$

a=-2

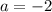
Putting
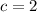c=2 in (v), we get

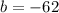
$b=-\dfrsc{6}{2}$

b=-3

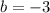
Therefore, the values of a,b,c are
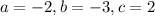a=-2,b=-3,c=2 .