Slope can be found using the following equation:
slope (m) =
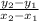
7) Let:
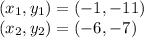
Plug in the corresponding numbers to the corresponding variables:
m =
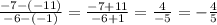
Slope:
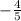
8) Let:
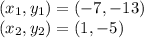
Plug in the corresponding numbers to the corresponding variables:
m =
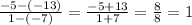
Slope:

9) Let:
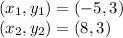
Plug in the corresponding numbers to the corresponding variables:
m =
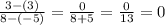
Slope:
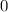
10) Let:
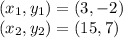
Plug in the corresponding numbers to the corresponding variables:
m =
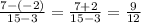
Simplify the slope. Divide common factors from both the numerator and denominator:
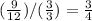
Slope:
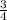
11) Let:
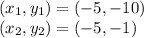
Plug in the corresponding numbers to the corresponding variables:
m =
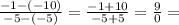 undefined.
undefined.
Slope: undefined
12) Let:
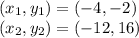
Plug in the corresponding numbers to the corresponding variables:
m =
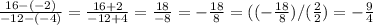
Slope:
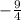
~