Answer:
The answer is "0.500".
Explanation:
The chance that round will be won,
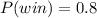
The likelihood of losing round by complementary law
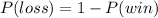
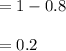
Let X be the number of rounds to the first loss played.
Here,
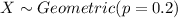
The PMF of X is the following:

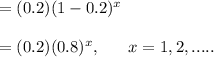
The mean of X is the geometric random variable property,
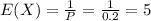
Markov's Inequality:
Suppose X is any random variable that has no negatives. So,
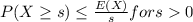
Find the upper bound of
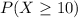
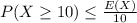
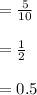
The highest probability is, therefore, that Markov's inequality will win at least ten rounds: 0.500