Question

Choose all of the points that are reflections of each other across both axes. (1.5,−2) ( 1 . 5 , - 2 ) and (−112,2) ( - 1 1 2 , 2 ) (4.5,−2) ( 4 . 5 , - 2 ) and (5.4,−2) ( 5 . 4 , - 2 ) (−112,3) ( - 1 1 2 , 3 ) and (−3,112) ( - 3 , 1 1 2 ) (1.75,−4) ( 1 . 75 , - 4 ) and (−134,4) ( - 1 3 4 , 4 )

Answer 1

The points which are reflections across both axis are;

1) (1.5, -2) and
`\left (-1(1)/(2) , \ 2\right )`

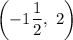
2) (1.75, -4) and
`\left (-1(3)/(4) , \ 4\right )`

Explanation:

The coordinate of the image of a point after a reflection across the 'x' and 'y' axis are given as follows;

`\begin{array}{ccc}& Preimage&Image\\Reflection \ about \ the \ x-axis&(x, \ y)&(x, \, -y)\\Reflection \ about \ the \ y-axis&(x, \ y)&(-x, \, y)\end{array}`

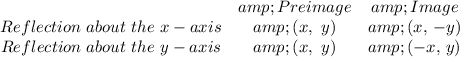
Therefore, a reflection across both axis changes (only) the 'x' and 'y' value signs

The given points which are reflections across both axis are;

(1.5, -2) and
`\left (-1(1)/(2) , \ 2\right )`

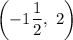
We note that
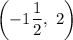`\left (-1(1)/(2) , \ 2\right )` = (-1.5, 2)

The reflection of (1.5, -2) across the x-axis gives the image (1.5, 2)

The reflection of the image (1.5, 2) across the y-axis gives the image (-1.5, 2)

Similarly, we have;

(1.75, -4) and
`\left (-1(3)/(4) , \ 4\right )`

We note that
`\left (-1(3)/(4) , \ 4\right )` = (-1.75, 4)

The reflection of (1.75, -4) across the x-axis gives the image (1.75, 4)

The reflection of the image (1.75, 4) across the y-axis gives the image (-1.75, 4).

The other points have changes in the values of the 'x' and 'y' between the given pair and are therefore not reflections across both axis