Answer:
66°
Explanation:
It is given that :
Distance of the satellite from the tower = 2000 m
Height of the satellite above the tower = 4500 m
Therefore the angle of elevation can be found out by :
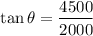
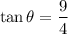
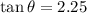
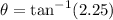
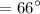
Therefore the tower can make contact with GPS satellite when it pointed at 66° angle.