Answer:
The answer is 30+7i.
Explanation:
Imaginary Number Definition
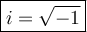
Simply evaluate like how you evaluate polynomials. Expand the expression in.
![\large{(8-3i)(3+2i)=[(8*3)+(8*2i)]+[(-3i*3)+(-3i*2i)]}\\\large{(8-3i)(3+2i)=(24+16i)+(-9i-6i^2)](https://img.qammunity.org/2022/formulas/mathematics/college/7ci7lfp2zjtcsl13jfcwfrbwh2i86vc3q2.png)
Therefore, our new expression when cancelling out the brackets is:
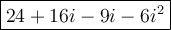
Imaginary Number Definition II
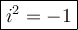
Therefore, substitute or change i² to -1
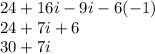
Complex Number Definition

Where a = Real Part and bi = Imaginary Part.
Therefore, it's the best to arrange in the form of a+bi.
Hence, the answer is 30+7i.