Question:-
Find the coordinates of the point which divides the join of (-1,7) and (4,-3) in the ratio 2:3 ?
Solution:-
Let the given points be A(-1,7) and B(4,-3)
Now,
Let the point be P(x, y) which divides AB in the ratio 2:3
Here,
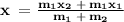
Where,
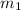 = 2 ,
= 2 ,
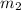 = 3
= 3
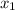 = -1 ,
= -1 ,
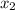 = 4
= 4
 Putting values we get,
Putting values we get,
x =
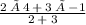
x =
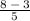
x =

x = 1
Now,
Finding y
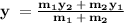
Where,
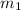 = 2 ,
= 2 ,
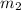 = 3
= 3
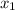 = 7 ,
= 7 ,
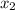 = -3
= -3
 Putting values we get,
Putting values we get,
y =
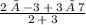
y =
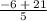
y =
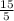
y = 3
Hence x = 1, y = 3
So, the required point is P(x, y)
= P(1, 3)
The coordinates of the point is P(1, 3). [Answer]
_______________________________________
Note:- Refer the attachment.
_______________________________________