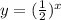1 Answer

Zara Kolagar · Answer 1 · 2022-09-02T21:28:45+0000

Answer:

$D.\ (3,(1)/(8))$

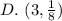
Explanation:

Given

y = ((1)/(2))^x

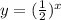
Required

Points that lies on the above graph

From the given options, only option D lies on the point and the proof is as follows:

$D.\ (3,(1)/(8))$

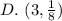
This means that:

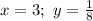
$x = 3;\ y = (1)/(8)$

Substitute
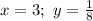$x = 3;\ y = (1)/(8)$ in
y = ((1)/(2))^x

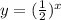
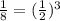
(1)/(8) = ((1)/(2))^3

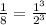
(1)/(8) = (1^3)/(2^3)

(1)/(8) = (1)/(8)

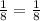
See that the values at the right and left hand side of the equation are the same.

This means that,
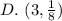$D.\ (3,(1)/(8))$ lies on
y = ((1)/(2))^x

Please log in or register to add a comment.