Given:
The graph of a trend line.
To find:
The equation of the trend line is slope intercept form.
Solution:
From the given graph it is clear that the equation of the trend line is passes through the points (0,25) and (5,50).
Slope of the line is:
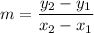
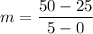
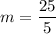
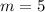
The line passes through the point (0,25). So, the y-intercept of the line is 25.
Slope intercept form of a line is:
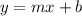
Where, m is slope and b is y-intercept.
The slope intercept from of the line is:
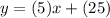
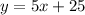
Therefore, the equation for the trend line in slope -intercept form is
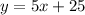 .
.