Question

Calculus helpppppppppppppppp

Answer 1

`\displaystyle y' = \frac{5x^2 + 3}{3(1 + x^2)^\bigg{(2)/(3)}}`

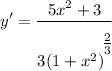
General Formulas and Concepts:

Pre-Algebra

• Equality Properties

Algebra I

• Functions
• Function Notation
• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Algebra II

• Logarithms and Natural Logs
• Logarithmic Property [Multiplying]:
  `\displaystyle log(ab) = log(a) + log(b)`
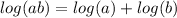
• Logarithmic Property [Exponential]:
  `\displaystyle log(a^b) = b \cdot log(a)`

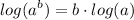
Calculus

Derivatives

Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Logarithmic Derivative:
`\displaystyle (d)/(dx) [lnu] = (u')/(u)`

Implicit Differentiation

Explanation:

Step 1: Define

Identify

`\displaystyle y = x\sqrt[3]{1 + x^2}`

Step 2: Rewrite

1. [Equality Property] ln both sides:
   `\displaystyle lny = ln(x\sqrt[3]{1 + x^2})`
2. Logarithmic Property [Multiplying]:
   `\displaystyle lny = ln(x) + ln(\sqrt[3]{1 + x^2})`
3. Exponential Rule [Root Rewrite]:
   `\displaystyle lny = ln(x) + ln \bigg[ (1 + x^2)^\bigg{(1)/(3)} \bigg]`
4. Logarithmic Property [Exponential]:
   `\displaystyle lny = ln(x) + (1)/(3)ln(1 + x^2)`

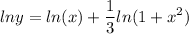
Step 3: Differentiate

1. ln Derivative [Implicit Differentiation]:
   `\displaystyle (d)/(dx)[lny] = (d)/(dx) \bigg[ ln(x) + (1)/(3)ln(1 + x^2) \bigg]`
2. Rewrite [Derivative Property - Addition]:
   `\displaystyle (d)/(dx)[lny] = (d)/(dx)[ln(x)] + (d)/(dx) \bigg[ (1)/(3)ln(1 + x^2) \bigg]`
3. Rewrite [Derivative Property - Multiplied Constant]:
   `\displaystyle (d)/(dx)[lny] = (d)/(dx)[ln(x)] + (1)/(3)(d)/(dx)[ln(1 + x^2)]`
4. ln Derivative [Chain Rule]:
   `\displaystyle (y')/(y) = (1)/(x) + (1)/(3) \bigg( (1)/(1 + x^2) \bigg) \cdot (d)/(dx)[(1 + x^2)]`
5. Rewrite [Derivative Property - Addition]:
   `\displaystyle (y')/(y) = (1)/(x) + (1)/(3) \bigg( (1)/(1 + x^2) \bigg) \cdot \bigg( (d)/(dx)[1] + (d)/(dx)[x^2] \bigg)`
6. Basic Power Rule]:
   `\displaystyle (y')/(y) = (1)/(x) + (1)/(3) \bigg( (1)/(1 + x^2) \bigg) \cdot (2x^(2 - 1))`
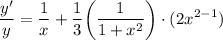
7. Simplify:
   `\displaystyle (y')/(y) = (1)/(x) + (1)/(3) \bigg( (1)/(1 + x^2) \bigg) \cdot 2x`
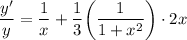
8. Multiply:
   `\displaystyle (y')/(y) = (1)/(x) + (2x)/(3(1 + x^2))`
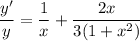
9. [Multiplication Property of Equality] Isolate y':
   `\displaystyle y' = y \bigg[ (1)/(x) + (2x)/(3(1 + x^2)) \bigg]`
10. Substitute in y:
    `\displaystyle y' = x\sqrt[3]{1 + x^2} \bigg[ (1)/(x) + (2x)/(3(1 + x^2)) \bigg]`
11. [Brackets] Add:
    `\displaystyle y' = x\sqrt[3]{1 + x^2} \bigg[ (5x^2 + 3)/(3x(1 + x^2)) \bigg]`
12. Multiply:
    `\displaystyle y' = \frac{(5x^2 + 3)\sqrt[3]{1 + x^2}}{3(1 + x^2)}`
13. Simplify [Exponential Rule - Root Rewrite]:
    `\displaystyle y' = \frac{5x^2 + 3}{3(1 + x^2)^\bigg{(2)/(3)}}`

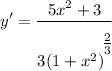
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Implicit Differentiation

Book: College Calculus 10e