Answer:
The nth term is
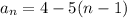
The 60th term of the sequence is -291.
Explanation:
Arithmetic sequence:
In an arithmetic sequence, the difference between consecutive terms is always the same, and it is called common difference.
The nth term is given by:
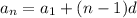
In which
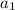 is the first term and d is the common difference.
is the first term and d is the common difference.
4,-1,-6
The common difference is:

First term
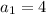
So
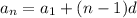
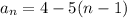
60th term:
 . Si
. Si
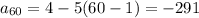
The 60th term of the sequence is -291.