Question

Write a polynomial equation for a graph that passes through the point (-1, 60) and has three x-intercepts: (-4,0),

(1, 0), and (3, 0)

Answer 1

Given:

A graph of a polynomial passes through the point (-1, 60) and has three x-intercepts: (-4,0), (1, 0), and (3, 0).

To find:

The equation of the polynomial.

Solution:

A polynomial is defined as:

`P(x)=a(x-c_1)(x-c_2)...(x-c_n)`

Where, a is a constant and
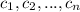`c_1,c_2,...,c_n` are the zeros of the polynomial.

The given polynomial has three x-intercepts (-4,0), (1, 0), and (3, 0). It means
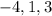`-4,1,3` are the zeroes of the given polynomial and
`(x+4),(x-1),(x-3)` are the factors of the given polynomial.

So, the equation of the polynomial is:

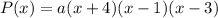`P(x)=a(x+4)(x-1)(x-3)` ...(i)

It passes through the point
`(-1,60)`.

`60=a(-1+4)(-1-1)(-1-3)`

`60=a(3)(-2)(-4)`

`60=24a`

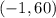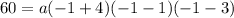
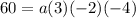
Divide both sides by 24.

`(60)/(24)=a`

`2.5=a`

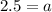
Putting
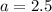`a=2.5` in (i), we get

`P(x)=2.5(x+4)(x-1)(x-3)`

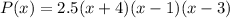
Therefore, the equation of the given polynomial is
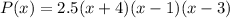`P(x)=2.5(x+4)(x-1)(x-3)`.