Given:
The given vector is:
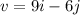
To find:
The unit vector in the direction of the given vector.
Solution:
If a vector is
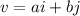 , then the unit vector in the direction of the this vector is
, then the unit vector in the direction of the this vector is
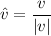
Where,
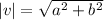
We have,
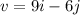
Here,
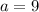 and
and
 . So,
. So,
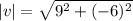
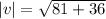
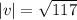
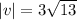
Now, the unit vector in the direction of the given vector is:
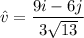
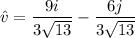
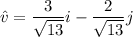
Therefore, the required unit vector is
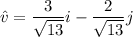 .
.