Answer:
The equation of the ellipse is
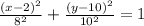 .
.
Explanation:
The statement is incomplete, the most probable outcome may be the equation of the ellipse based on information given.
The equation of an ellipse whose major axis is vertical and is centered at a point different from origin is defined by:
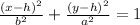 (1)
(1)
Where:
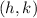 - Coordinates of the center of the ellipse.
- Coordinates of the center of the ellipse.
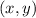 - Coordinates of a point in the line of the ellipse.
- Coordinates of a point in the line of the ellipse.
 - Length of the major semiaxis.
- Length of the major semiaxis.
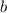 - Length of the minor semiaxis.
- Length of the minor semiaxis.
The coordinates of the center of the ellipse is midpoint of the segment between vertices, which are collinear with foci:
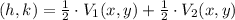 (1)
(1)
Where
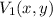 and
and
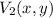 are the coordinates of the vertices.
are the coordinates of the vertices.
If we know that
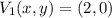 and
and
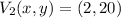 , then the coordinates of the center ellipse are:
, then the coordinates of the center ellipse are:
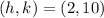
The length of the semimajor axis can be determined by using the following vectorial expression, which is equivalent to the Pythagorean Theorem:
![a = \sqrt{[(h,k)-V_(1)(x,y)]\,\bullet\,[(h,k)-V_(1)(x,y)]}](https://img.qammunity.org/2022/formulas/mathematics/high-school/co4c276wttz7to5if0llicxzt41oglwdza.png) (2)
(2)
If we know that
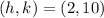 and
and
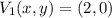 , then the length of the semimajor axis is:
, then the length of the semimajor axis is:
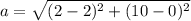
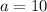
And the length of the minor semiaxis is found by means of this Pythagorean identity:
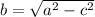 (3)
(3)
Where
 is the length between the center and any of the foci. This distance can be found by using this vectorial formula:
is the length between the center and any of the foci. This distance can be found by using this vectorial formula:
![c = \sqrt{[(h,k)-F_(1)(x,y)]\,\bullet\,[(h,k)-F_(1)(x,y)]}](https://img.qammunity.org/2022/formulas/mathematics/high-school/ed3iofh6tvgfc7f5i0tqq30ju55eenp8d1.png) (4)
(4)
If we know that
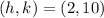 and
and
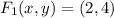 , then the length between the center and any of the foci is:
, then the length between the center and any of the foci is:
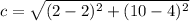
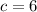
And the length of the minor semiaxis is:
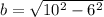
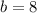
FInally, the equation of the ellipse is
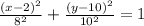 .
.