Answer:
The length of the other two sides are: 43.09 and 32.60
Explanation:
Let the given side of the triangle be b(= 40), and the angles be;
A =
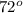 , B =
, B =
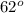 and C =
and C =
 .
.
Applying the Sine rule,
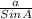 =
=
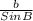 =
=
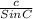
So that,
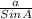 =
=
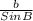
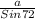 =
=
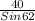
a =

= 43.0898
a = 43.09
Also,
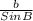 =
=
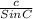
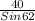 =
=
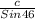
c =
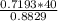
= 32.5881
c = 32.60
The length of the other two sides are: 43.09 and 32.60