Question

A person invests 8000 dollars in a bank. The bank pays 7% interest compounded

annually. To the nearest tenth of a year, how long must the person leave the money
in the bank until it reaches 15600 dollars?
nt
A=P(1+
)
п

Answer 1

The person must leave the money for around 9.9 years.

General Formulas and Concepts:
Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Terms/Coefficients

Compounded Interest Rate Formula:
`\displaystyle A = P \bigg( 1 + (r)/(n) \bigg)^(nt)`

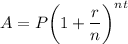
• P is principle amount (initial amount)
• r is interest rate
• n is compounded rate
• t is time (in years)

Algebra II

Logarithms

• Logarithmic Property [Exponential]:
  `\displaystyle \log (a^b) = b \cdot \log (a)`

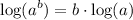
Explanation:

Step 1: Define

Identify variables.

A = $15600

P = $8000

r = 0.07

n = 1

Step 2: Find Time Elapsed

1. Substitute in variables [Compounded Interest Rate Formula]:
   `\displaystyle 15600 = 8000 \bigg( 1 + (0.07)/(1) \bigg)^(1(t))`
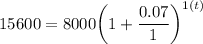
2. [Exponents] Simplify:
   `\displaystyle 15600 = 8000 \bigg( 1 + (0.07)/(1) \bigg)^(t)`
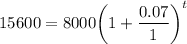
3. (Parenthesis) Simplify:
   `\displaystyle 15600 = 8000(1.07)^(t)`
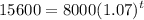
4. [Division Property of Equality] Divide 8000 on both sides:
   `\displaystyle (39)/(20) = (1.07)^(t)`
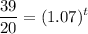
5. [Equality Property] Log both sides:
   `\displaystyle \log (39)/(20) = \log (1.07)^(t)`
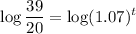
6. Simplify [Logarithm Property - Exponential]:
   `\displaystyle \log (39)/(20) = t \log (1.07)`
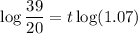
7. [Division Property of Equality] Isolate t:
   `\displaystyle t = (\log (39)/(20))/(\log 1.07)`
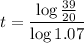
8. Evaluate:
   `\displaystyle t = 9.87057`
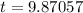
9. Round:
   `\displaystyle t \approx 9.9`

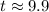
∴ it will take the person approximately 9.9 years investing $8,000 with a 7% interest rate compounded annually for them to obtain $15,600.

---

Topic: Algebra II