Question

A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. At one point in its motion its kinetic energy is K = 5 J ànd its potential energy (measured with U = 0 at x = Q) is U = 3 J. When it is at x =xm the kinetic and potential energies are:

Answer 1

ummm i dk what your asking

Step-by-step explanation:

Answer 2

At the amplitude
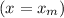`(\(x = x_m\))\\` in simple harmonic motion, kinetic energy
`(\(K\))`is zero, and potential energy (\(U\)) is equal to the total mechanical energy
`(\(E = 8 \, \text{J}\)).\\`

In simple harmonic motion, the total mechanical energy (sum of kinetic and potential energies) remains constant. The total mechanical energy
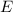`\(E\)` is given by:

`\[ E = K + U \]`

Given that at one point in the motion, kinetic energy
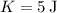`\(K = 5 \, \text{J}\)` and potential energy
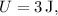`\(U = 3 \, \text{J}\),` the total mechanical energy at that point is:

`\[ E = 5 \, \text{J} + 3 \, \text{J} = 8 \, \text{J} \]`

At any point in simple harmonic motion, the total mechanical energy is also related to the potential energy and kinetic energy as follows:

`\[ E = K + U \]`

Now, when the particle is at the amplitude
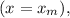`(\(x = x_m\)),\\` the potential energy is maximum, and the kinetic energy is zero. Therefore, at
`\(x = x_m\),\\` the potential energy
`(\(U_{\text{max}}\))\\` is equal to the total mechanical energy, and the kinetic energy (\(K_{\text{max}}\)) is zero:

`\[ U_{\text{max}} = E \]`

`\[ K_{\text{max}} = 0 \]\\`

So, at
`\(x = x_m\),\\` the kinetic and potential energies are:

`\[ K_{\text{max}} = 0 \, \text{J} \]\\`

`\[ U_{\text{max}} = 8 \, \text{J} \]\\`