Question

Solve for x. Round to the nearest tenth of a degree, if necessary.

S
8.8
70
T
13
U

Answer 1

The measure of angle
`\( x \)` in the triangle. 
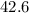`42.6` degrees

the step-wise calculation to find the angle
`\( x \)` in the triangle:

Step 1: Identify the sides

In the right-angled triangle, we are given:

- The length of the opposite side to angle
`\( x \)`: 8.8 units

- The length of the hypotenuse: 13 units

We want to find the measure of angle
`\( x \)` using these lengths.

Step 2: Find the adjacent side

Since we are given the hypotenuse and the opposite side, we need to find the length of the adjacent side to use the tangent function. We can find the adjacent side using the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (\( c \)) is equal to the sum of the squares of the lengths of the other two sides (\( a \) and \( b \)):

`\[ c^2 = a^2 + b^2 \]`

In our case,
`\( c \)` is the hypotenuse (13 units), and
`\( a \)` is the opposite side (8.8 units). We want to find
`\( b \)`, the adjacent side:

`\[ b = √(c^2 - a^2) \]`

`\[ b = √(13^2 - 8.8^2) \]`

`\[ b = √(169 - 77.44) \]`

`\[ b = √(91.56) \]`

`\[ b \approx 9.57 \]` units

Step 3: Calculate the angle using the tangent function

Now, we will use the tangent function to find the angle
`\( x \)`. The tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side:

`\[ \tan(x) = \frac{\text{opposite}}{\text{adjacent}} \]`

`\[ \tan(x) = (8.8)/(9.57) \]`

`\[ \tan(x) \approx 0.9195 \]`

Step 4: Find the angle

To find angle
`\( x \)`, we need to take the arctangent (inverse tangent) of the ratio we just calculated:

`\[ x = \arctan(0.9195) \]`

`\[ x \] (in radians) \( \approx 0.7441 \)`

Step 5: Convert to degrees

Since we often measure angles in degrees, we need to convert the angle from radians to degrees:

`\[ x \] (in degrees) \( = \frac{0.7441 \text{ radians}}{1 \text{ radian}} * (180)/(\pi) \text{ degrees} \)`

`\[ x \] (in degrees) \( \approx 42.6448 \)`

Step 6: Round to the nearest tenth

Finally, we round the angle to the nearest tenth of a degree:

`\[ x \] (rounded) \( = 42.6 \)` degrees

This gives us the measure of angle
`\( x \)` in the triangle.

Answer 2

Use law of sines:

Cos(x) = adjacent/ hypotenuse

cos(x) = 8.8/13

X = arcsin(8.8/13)

X = 47.396 degrees

Rounded to the nearest tenth = 37.4 degrees