The measure of angle
 in the triangle.
in the triangle.
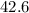 degrees
degrees
the step-wise calculation to find the angle
 in the triangle:
in the triangle:
Step 1: Identify the sides
In the right-angled triangle, we are given:
- The length of the opposite side to angle
 : 8.8 units
: 8.8 units
- The length of the hypotenuse: 13 units
We want to find the measure of angle
 using these lengths.
using these lengths.
Step 2: Find the adjacent side
Since we are given the hypotenuse and the opposite side, we need to find the length of the adjacent side to use the tangent function. We can find the adjacent side using the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (\( c \)) is equal to the sum of the squares of the lengths of the other two sides (\( a \) and \( b \)):
![\[ c^2 = a^2 + b^2 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/nw83braw9rnc36xktpoi.png)
In our case,
 is the hypotenuse (13 units), and
is the hypotenuse (13 units), and
 is the opposite side (8.8 units). We want to find
is the opposite side (8.8 units). We want to find
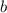 , the adjacent side:
, the adjacent side:
![\[ b = √(c^2 - a^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/b2j6fueiwb2ervgtz7ia.png)
![\[ b = √(13^2 - 8.8^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/w83piureccsh21gjzco1.png)
![\[ b = √(169 - 77.44) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/kyd1uglvyxiifq9m4shq.png)
![\[ b = √(91.56) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/gcrgi8szkvx4mtcmy4q6.png)
![\[ b \approx 9.57 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/eyv2b2qh1khsmbtd0j09.png) units
units
Step 3: Calculate the angle using the tangent function
Now, we will use the tangent function to find the angle
 . The tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side:
. The tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side:
![\[ \tan(x) = \frac{\text{opposite}}{\text{adjacent}} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/qsb4w3y7mmdb40qqaui4.png)
![\[ \tan(x) = (8.8)/(9.57) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/mvr77cq0k0zxf8lveqqc.png)
![\[ \tan(x) \approx 0.9195 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/6lwixzu0zaphu6ojpmo6.png)
Step 4: Find the angle
To find angle
 , we need to take the arctangent (inverse tangent) of the ratio we just calculated:
, we need to take the arctangent (inverse tangent) of the ratio we just calculated:
![\[ x = \arctan(0.9195) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/2oaphxd2dlpguqbvkdbm.png)
![\[ x \] (in radians) \( \approx 0.7441 \)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/7soe0mdtakprveuv12kt.png)
Step 5: Convert to degrees
Since we often measure angles in degrees, we need to convert the angle from radians to degrees:
![\[ x \] (in degrees) \( = \frac{0.7441 \text{ radians}}{1 \text{ radian}} * (180)/(\pi) \text{ degrees} \)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/lmvqtqqa0bcbz9v263xi.png)
![\[ x \] (in degrees) \( \approx 42.6448 \)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/oks97d352n1pmcx2iuc9.png)
Step 6: Round to the nearest tenth
Finally, we round the angle to the nearest tenth of a degree:
![\[ x \] (rounded) \( = 42.6 \)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/fsn56h08vs90l19xl6aa.png) degrees
degrees
This gives us the measure of angle
 in the triangle.
in the triangle.