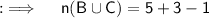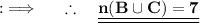We are provided with ;
And we need no find
 . At first Let me tell you that here
. At first Let me tell you that here
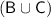 represents the union of the set B and C.And
represents the union of the set B and C.And
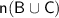 represents the cardinal no. of the respective set or no. of elements present in the respective set.So let's find the set
represents the cardinal no. of the respective set or no. of elements present in the respective set.So let's find the set
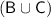 first
first
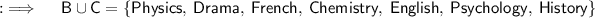
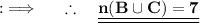
Alternative Method :-
As we know that ;
Where
 is the Intersection of A and B or the set of common elements of A and B. So now by same concept , now finding the intersection of B and C :-
is the Intersection of A and B or the set of common elements of A and B. So now by same concept , now finding the intersection of B and C :-
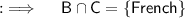
So ,
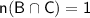 . Now , putting the values in the formula;
. Now , putting the values in the formula;