Question

An object has a weight of 1550N when it is on the surface of a planet of radius R. What will be the gravitational force on the object after it has been moved to a distance of 4R from the surface of the planet?

Answer 1

W = 96.875 N

Step-by-step explanation:

For this exercise let's use the law of universal gravitation

F =
`G (m M )/(r^2)`

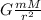
we substitute this force in Newton's second law

F = m a

G \frac{m M }{r^2} = m a

a =
`G (M)/(r^2)`

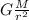
This sidewalk we will call it gravity acceleration

g₀ = a

the weight of a body is

W₀ = m g₀

if we change the cario of r ’= 4r

a’=
`G (M)/(r'^2 )`

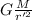
a ’= G \frac{M}{(4r)^2 }

a' =
`G (M)/(r^2) \ (1)/(16)`

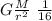
a ’=
`(g_o)/(16)`

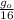
therefore the weight of the body must be

W = m g =
`m \ (g_o)/(16)`

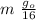
W = W₀ / 16

W = 1550/16

W = 96.875 N