PLEASE Answer asap!!!!

Question

asked Oct 20, 2022 11.3k views

1 Answer

Lin Song Yang · Answer 1 · 2022-10-25T03:14:19+0000

Answer:

x=0

Explanation:

The axis of symmetry:
x=(-b)/(2a) when the equation is
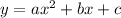
y=ax^2+bx+c

The given equation is:

y=x^2-6

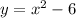
To make the a and b values more easily identifiable, we can rewrite it like this:

y=1x^2+0-6

Now, we can tell that a=1 and b=0. Plug these into the equation
x=(-b)/(2a) :

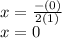
$x=(-(0))/(2(1))\\x=0$

Therefore, the equation for the axis of symmetry for the parabola is x=0.

I hope this helps!