Question

Para decorar una pared se disponen de tiras de papel azules de 15 cm, verdes de 20 cm, y rojas de 25 cm. En la pared se quiere armar tres líneas del mismo tamaño, una de cada color y sin cortar ninguna tira. a) ¿Cuánto va a medir la menor línea que se puede armar con cada color? b) ¿Cuántas tiras se deben utilizar? c) ¿Cuántas de cada color?

Answer 1

a) Smallest line that can be made with each color = 300 cm

b) Total strips should be used = 47 strips

c) Total strips used of blue color = 20

Total strips used of green color = 15

Total strips used of red color = 12

Explanation:

Given - To decorate a wall, there are 15 cm blue, 20 cm green, and 25 cm red strips of paper. On the wall you want to build three lines of the same size, one of each color and without cutting any strip.

To find - a) How long is the smallest line that can be made with each color?

b) How many strips should be used?

c) How many of each color?

Proof -

a)

For the smallest line that can be made with each color, we just have to find the lcm (least common multiple) of the 3 srtips.

Firstly,

Decompose the 3 strips to its prime factors , we get

15 = 3×5

20 = 2²×5

25 = 5²

So,

The Lcm(15, 20, 25) = 3×2²×5² = 3×4×25 = 300

∴ we get

Smallest line that can be made with each color = 300 cm

b)

Now,

Total strips used = 300 cm

Strips used by 15 cm blue =
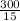`(300)/(15)` = 20 strips

Strips used by 20 cm green =
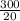`(300)/(20)` = 15 strips

Strips used by 25 cm red =
`(300)/(25)` = 12 strips

So,

Total strips should be used = 20 + 15 + 12 = 47 strips

c)

Total strips used of blue color = 20

Total strips used of green color = 15

Total strips used of red color = 12