We are given with a inequality and we have to find the solution for it . So , let's start :
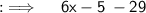
Adding 5 to both sides :
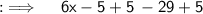
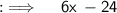
Dividing both sides by 6 ;
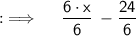

Hence , Option A) x > - 4 is correct :D
Note :-
Whenever dividing or multiplying an inequality by a -ve , so we have to tilt the sign too , while if we are multiplying or dividing with a +ve , so sign will remain the same , For example like if we are given with x > y , and we multiply both sides by -1 . So , it will then become - x < - y