Answer:
0.9728
Explanation:
We have 2 options for the system to fail - no components work, or only one works.
The probability that no components work is:
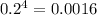
The probability that one SPECIFIC component works and the others failed is:
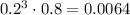
And because there's 4 components, the chance that EXACTLY ONE works but the others don't is:
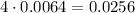
So we sum the probabilities:
