Question

In Exercises 1-4, the sample size n, probability of success p, and probability of

failure q are given for a binomial experiment. Determine whether you can use a
normal distribution to approximate the distribution of x.
1. n = 24, p = 0.85, 9 = 0.15
2. n = 15, p = 0.70, q = 0.30
3. n = 18, p = 0.90, q = 0.10
4. n = 20, p = 0.65, q = 0.35

Answer 1

1. No

2. No

3. No

4. Yes

Explanation:

Binomial approximation to normal.

The binomial probability distribution has parameters n, p and q.

If

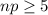`np \geq 5` and
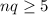`nq \geq 5`, you can use the normal approximation.

1. n = 24, p = 0.85, q = 0.15

`np = 24*0.85 = 20.4 > 5`

`nq = 24*0.15 = 3.6 < 5`

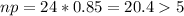
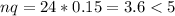
So no.

2. n = 15, p = 0.70, q = 0.30

`np = 15*0.7 = 10.5 > 5`

`nq = 15*0.3 = 4.5 < 5`

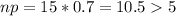
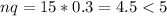
So no.

3. n = 18, p = 0.90, q = 0.10

`np = 18*0.9 = 16.2 > 5`

`nq = 18*0.1 = 1.8 < 5`

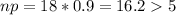
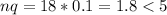
No

4. n = 20, p = 0.65, q = 0.35

`np = 20*0.65 = 13 > 5`

`nq = 20*0.35 = 7 > 5`

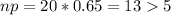
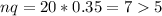
Yes