Answer: a 95% confidence interval for the proportion of all customers who have experienced a service interruption: (0.076, 0.127).
Explanation:
Let p be the population proportion of all customers who have experienced a service interruption.
Confidence interval for p:
 , where
, where
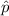 = sample proportion, n= sample size, z* = critical z-value.
= sample proportion, n= sample size, z* = critical z-value.
Given: n = 540
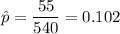
z* = 1.96
The required confidence interval:

Hence, a 95% confidence interval for the proportion of all customers who have experienced a service interruption: (0.076, 0.127).