Question

The driver of a car wishes to pass a truck that is traveling at a constant speed of 19.3 m/s . Initially, the car is also traveling at a speed 19.3m/s and its front bumper is a distance 25.0m behind the truck's rear bumper. The car begins accelerating at a constant acceleration 0.560m/s^2 , then pulls back into the truck's lane when the rear of the car is a distance 26.5m ahead of the front of the truck. The car is of length 4.50m and the truck is of length 20.7m .

Part A) How much time is required for the car to pass the truck?
Part B ) What distance does the car travel during this time?
Part C) What is the final speed of the car?

Answer 1

A) t = 10.56 s, B) x = 235 m, C) v = 25.2 m / s

Step-by-step explanation:

A) We can solve this problem using kinematics expressions.

The distance traveled by the truck is

x_c = v_c t

Distance traveled by the car.

The car must travel the distance that separates them from the truck x₀=25.0. Return to the lane at x₁ = 26.5 m. the length of the truck x₂=20.7m and the length of the car x₃ = 2 4.5 = 9 m, therefore the total length traveled by the car is

x_t = x₁ + x₂ + x₃

x_t = 26.5 + 20.7 +9 = 56.2 m

the distance traveled by the car when it returns to the lane is

x_c + x_t = x₀ + v₀ t + ½ a t²

when the car passes the car the distance traveled by the two vehicles is the same, we substitute

v_c t + x_t = x₀ + v₀ t + ½ a t²

½ a t² + t (v₀ -v_c) + (x₀ - x_t) = 0

we substitute the values

½ 0.560 t² + t (19.3 -19.3) + (25.0 - 56.2) =

0.28 t² -31.2 = 0

t =
`\sqrt{ (31.2)/(0.28) }`

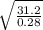
t = 10.56 s

This is the time it takes for the car to pass the truck and back into the lane.

B) the distance traveled is

x = v₀ t + ½ a t²

x = 19.3 10.56 + ½ 0.560 10.56²

x = 235 m

C) the final velocity is

v = v₀ + a t

v = 19.3 + 0.560 10.56

v = 25.2 m / s