Answer:
The variance of the times between accidents is of 1849 days squared.
Explanation:
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
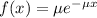
In which
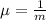 is the decay parameter.
is the decay parameter.
The variance of the exponential distribution is:
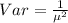
Assume that the mean time between accidents is 43 days.
This means that

What is the variance of the times between accidents?
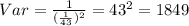
The variance of the times between accidents is of 1849 days squared.