Answer:
The final speed of the crate is 12.07 m/s.
Step-by-step explanation:
For the first 10.0 meters, the only force acting on the crate is 225 N, so we can calculate the acceleration as follows:
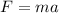
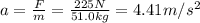
Now, we can calculate the final speed of the crate at the end of 10.0 m:
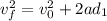
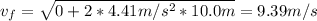
For the next 10.5 meters we have frictional force:
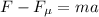
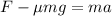
So, the acceleration is:
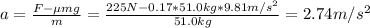
The final speed of the crate at the end of 10.0 m will be the initial speed of the following 10.5 meters, so:
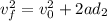
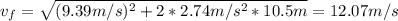
Therefore, the final speed of the crate after being pulled these 20.5 meters is 12.07 m/s.
I hope it helps you!