Question

Question 8: Unspooling Thread (100 points) A 110 g spool of thread with a 4.2 cm radius is held up by a peg through its center and allowed to freely rotate. Assume the thread is ideal (i.e., it does not stretch or slip, and its mass is negligibly small). A 160 g needle is tied to the loose end of the thread. The needle is dropped, and it accelerates to the floor as the thread unwinds. Find the tension in the thread and the magnitude of the acceleration of the needle as it falls.

Answer 1

a = 7.29 m / s², T = 0.40 N

Step-by-step explanation:

To solve this exercise we must apply Newton's second law to each body

The needle

W -T = m a

mg - T = ma

The spool, which we will approach by a cylinder

Σ τ = I α

T R = I α

the moment of inertia of a cylinder with an axis through its center is

I = ½ M R²

angular and linear variables are related

a = α R

α = a / R

we substitute

T R = (½ M R²) a / R

T = ½ M a

we write our system of equations together

mg - T = m a

T = ½ M a

we solve

m g = (m + ½ M) a

a =
`(m)/(m + (1)/(2) M) \ g`

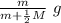
let's calculate

a =
`(0.160)/(0.160 + (1)/(2) 0.110) \ 9.8`

a = 7.29 m / s²

now we can look for the tension

T = ½ M a

T = ½ 0.110 7.29

T = 0.40 N