Answer:
The speed of the student just before she lands, v₂ is approximately 8.225 m/s
Step-by-step explanation:
The given parameters are;
The mass of the physic student, m = 43.0 kg
The height at which the student is standing, h = 12.0 m
The radius of the wheel, r = 0.300 m
The moment of inertia of the wheel, I = 9.60 kg·m²
The initial potential energy of the female student, P.E.₁ = m·g·h₁
Where;
m = 43.0 kg
g = The acceleration due to gravity ≈ 9.81 m/s²
h = 12.0 h
∴ P.E.₁ = 43 kg × 9.81 m/s² × 12.0 m = 5061.96 J
The kinetic rotational energy of the wheel and kinetic energy of the student supporting herself from the rope she grabs and steps off the roof, K₁, is given as follows;

The initial kinetic energy, 1/2·m·v₁² and the initial kinetic rotational energy, 1/2·m·ω₁² are 0
∴ K₁ = 0 + 0 = 0
The final potential energy of the student when lands. P.E.₂ = m·g·h₂ = 0
Where;
h₂ = 0 m
The final kinetic energy, K₂, of the wheel and student is give as follows;
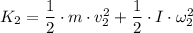
Where;
v₂ = The speed of the student just before she lands
ω₂ = The angular velocity of the wheel just before she lands
By the conservation of energy, we have;
P.E.₁ + K₁ = P.E.₂ + K₂
∴ m·g·h₁ +
 = m·g·h₂ +
= m·g·h₂ +
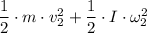
Where;
ω₂ = v₂/r
∴ 5061.96 J + 0 = 0 +
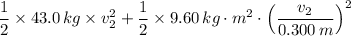
5,061.96 J = 21.5 kg × v₂² + 53.
 kg × v₂² = 21.5 kg × v₂² + 160/3 kg × v₂²
kg × v₂² = 21.5 kg × v₂² + 160/3 kg × v₂²
v₂² = 5,061.96 J/(21.5 kg + 160/3 kg) ≈ 67.643118 m²/s²
v₂ ≈ √(67.643118 m²/s²) ≈ 8.22454363 m/s
The speed of the student just before she lands, v₂ ≈ 8.225 m/s.