Given:
 is continuous,
is continuous,
 .
.
To find:
The value of
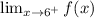 and
and
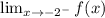 .
.
Solution:
If a function f(x) is continuous at
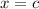 , then
, then
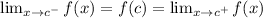
It is given that the function
 is continuous. It means it is continuous for each value and the left-hand and right-hand limits are equal to the value of the function.
is continuous. It means it is continuous for each value and the left-hand and right-hand limits are equal to the value of the function.
The function is continuous for 6. So,

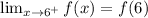
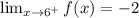
The function is continuous for -2. So,
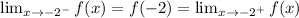
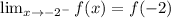
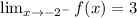
Therefore,
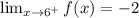 and
and
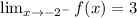 .
.