Answer:
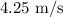
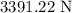
Step-by-step explanation:
y = Height of compression = 0.38 m
m = Mass of basketball player = 101 kg
h = Height of center of gravity after jump = 0.92 m
g = Acceleration due to gravity =
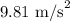
Energy balance of the system is given by
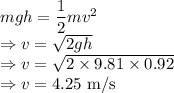
The velocity of the player when he leaves the floor is
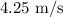
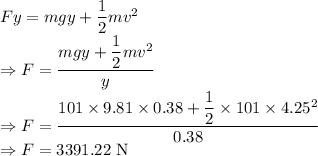
The force exerted on the floor is
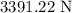 .
.