Question

Juanita is a 28-year old female college graduate from the South. Molly is a 28-year female college graduate from the West. Jennifer is a 28-year female college graduate from the Midwest. (i) Construct a 95% confidence interval for the difference in expected earnings between Juanita and Molly. (ii) Explain how you would construct a 95% confidence interval for the difference in expected earnings between Juanita and Jennifer.

Answer 1

Hello your question has some missing information attached below is the missing information

answer :

i) ( 0.158 , - 1.018 )

ii) the difference in expected earnings can be computed as

(
`X_(6,A) - X_(5,C) ) = \beta _(0) + \beta _(6) - ( \beta _(0) - \beta _(5) ) = \beta _(6) - \beta _(5)`

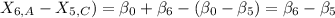
Explanation:

i) Construct a 95% confidence interval ( between Juanita and Molly )

Expected difference in earnings = ( X
`_(6)`
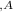`_(,A)` - X
`_(6.B)`) =
`\beta _(0)`= (
`\beta + \beta _(6)` )

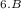∴ 95% confidence interval

-0.43 ± 1.96 * 0.30 = [ -0.43 ± 0.588 ] = ( 0.158 , - 1.018 ) ( hence confidence interval at 95% = 1.96 )

ii) Construct a 95% confidence interval ( between Juanita and Jennifer )

Juanita is a student from the south and Jennifer is a student from Midwest

therefore the difference in expected earnings can be computed as

(
`X_(6,A) - X_(5,C) ) = \beta _(0) + \beta _(6) - ( \beta _(0) - \beta _(5) ) = \beta _(6) - \beta _(5)`

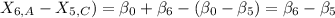
therefore a 95% confidence interval can be calculated with the above regression model.