Let's solve for value of values of x and y ~
According to Angle sum property of triangles :

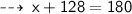
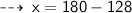
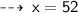
Now, solve for y ~
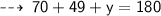


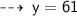
Now, by the results we got, we can conclude that :
The two triangles are not similar because 70 + 58 + x = 180 means x = 52° and 70 + 49 + y=180 means y = 61°