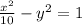Question

Nrite an equation of the ellipse with foci at (3, 0) and co-vertices at (0, +_1).

Answer 1

`\frac{ {x}^(2) }{10} + {y}^(2) = 1`

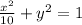
Explanation:

Equation of ellipse is

`\frac{(x - h) {}^(2) }{ {a}^(2) } + \frac{(y - k) {}^(2) }{ {b}^(2) } = 1`

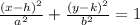
Where h,k is center

A is the length of semi-major axis. This axis include the foci

b is length of semi-minor axis. This axis includes main vertices.

Since we have 0,1 and 0,-1 as co-vertices, the length of the minor axis is 2 so the length of the semi-major is 1.

So we have now,

`\frac{(x - h) {}^(2) }{ {a}^(2) } + \frac{(y - k) {}^(2) }{1} = 1`

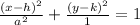
Next, to since the foci has a y coordinate of 0 and the co-vertrx has a x coordinate of 0, our center is 0,0

so we have

`\frac{ {x}^(2) }{ {a}^(2) } + {y}^(2) = 1`

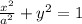
Now, we can do equation

`{a}^(2) - {b}^(2) = {c}^(2)`

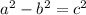
B^2=1

C^2 is 9

`{a}^(2) - 1 = 9`

`{a}^(2) = 10`

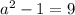
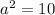
S0, we now have

`\frac{ {x}^(2) }{10} - {y}^(2) = 1`